“11.23” questa data, apparentemente uguale a tutte le altre, racchiude, per gli appassionati di matematica e numerologia, un significato in realtà molto importante. In essa sono presenti i primi termini della celeberrima serie di Fibonacci. Pertanto, oggi è il Fibonacci’s day, grande matematico italiano vissuto a cavallo tra il 1100 ed il 1200.
Leonardo Pisano detto il Fibonacci, in quanto letteralmente “figlio di Bonaccio”, è considerato uno dei più grande studiosi di matematica della storia, capace di rispolverare lo studio delle scienze esatte dopo il torpore del basso medioevo. A lui dobbiamo la scoperta della serie numerica più famosa della storia. La particolarità della successione di Fibonacci è quella di essere una serie di numeri interi, in cui ciascuno è la sommatoria dei primi due, fatta eccezione per i primi due termini in essa contenuti, “0 1 1 2 3 5 8 13….”.
Matematicamente si scrive che dati F0=n, e F1=1, allora Fn= Fn-1 + Fn-2. Il matematico italiano propose tale sequenza numerica come risposta al seguente quesito, proposto da Federico II di Svevia:
“Quante coppie di conigli si ottengono in un anno, salvo i casi di morte, supponendo che ogni coppia dia alla luce un’altra coppia ogni mese e che le coppie più giovani siano in grado di riprodursi già al secondo mese di vita?”.
Gli elementi di questa serie numerica sono di vario tipo, nel senso che vi si riscontrano sia numeri primi che numeri divisibili per diversi fattori. Ad oggi sono conosciuti solo 3 numeri della serie che sono anche quadrati, ovvero 0, 1 e 144. I numeri di Fibonacci vantano diverse proprietà e curiosità matematiche. Queste spaziano dal collegamento con il Triangolo di Tartaglia, che, se riscritto o traslato, permette di leggere come somma delle diagonali che lo compongono l’intera serie.
Il triangolo di Tartaglia è una disposizione geometrica di coefficienti binomiali a forma di triangolo. Dati 4 numeri di Fibonacci, il prodotto del primo con il quarto è uguale al prodotto del secondo con il terzo, maggiorato o diminuito di 1. Ancora, dato un numero di Fibonacci, esso è la sommatoria di tutti i numeri della sequenza che lo precedono, eccetto il penultimo, aumentata di 1 (regola definita dell’addizione fulminea).
Altra curiosità è quella del “diabolico undici”, nome derivante dal fatto che tale numero nel medioevo era considerato diabolico, poiché 11 oltrepassava finanche i 10 comandamenti. Questa regola prevede che, dati 10 numeri di Fibonacci, la loro sommatoria sia sempre divisibile per 11. Continuando, considerati 10 numeri della serie, la loro sommatoria è pari al settimo membro del gruppo prescelto moltiplicato per 11.
La successione numerica che prosegue all’infinito è definita anche successione aurea, perché il limite del rapporto tra un valore della serie ed il precedente tende ad un valore irrazionale, chiamato sezione aurea o numero di Fidia, pari a 1,618033987… Parimenti, il rapporto tra un elemento della serie di Fibonacci ed il suo successivo tende al reciproco del numero di Fidia ed è pari a 0,618033987. Alcuni studiosi definiscono la successione “il codice segreto della natura”. La sezione aurea, per definizione matematica, è la porzione più piccola (A) di una retta immaginaria divisa in due segmenti non di uguali misura. La particolarità sta nella proporzione matematica che la sezione segue, poiché essa sta al segmento più grande (B), come quest’ultimo sta all’intera retta (R). A:B=B:R. La sezione aurea si indica con Φ (phi), dal nome dell’architetto greco Fidia, che per primo ne calcolò il valore, anche se alcuni studiosi ne fanno risalire la conoscenza al VI secolo a.C. ed alla scuola pitagorica.
Si ritiene che fu Ippaso di Metaponto, allievo del genio crotonese, il primo a diffondere il valore della grandezza di phi. Questo valore è definito anche proporzione divina. La sua straordinarietà è quella di collegare in molteplici situazioni la matematica con la natura. Anche le applicazioni che ha trovato la successione di Fibonacci, partendo dalla riproduzione dei conigli, sono molteplici e riguardano i più disparati campi della scienza. Per fare qualche esempio, è stato osservato che il numero di giri che una pianta compie intorno ad un fusto per distanziare tra loro due foglie, è sempre un numero di Fibonacci. Ed il quoziente di fillotassi, cioè il rapporto tra numero di giri e numero di foglie presenti, è la sezione aurea.
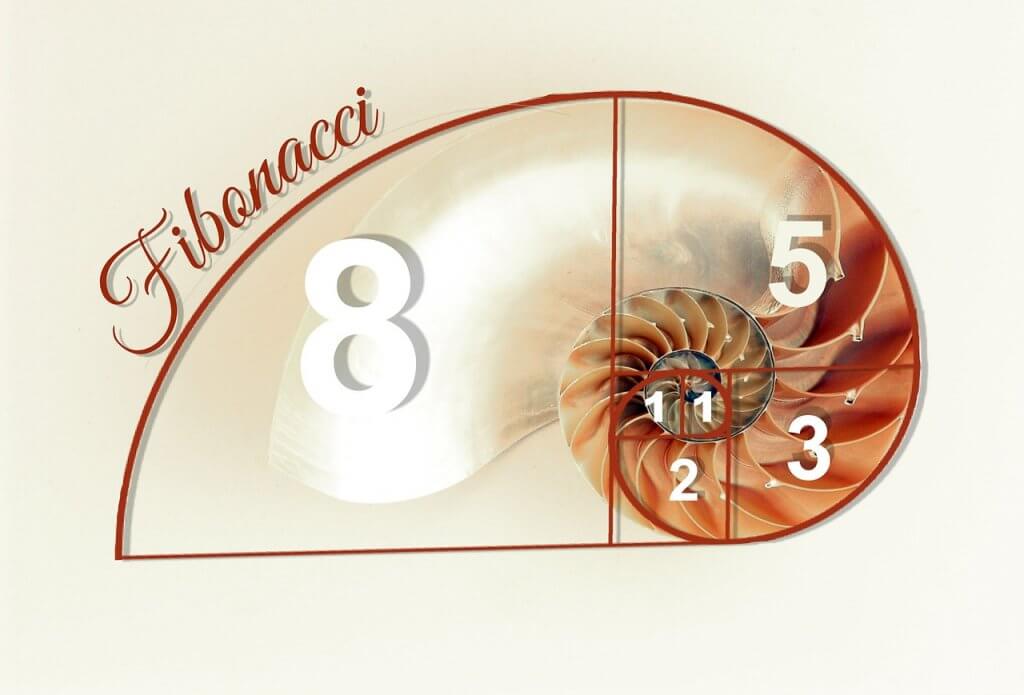
Ancora, la buccia dell’ananas è formata, solitamente, da 3 file di squame che sono rispettivamente, 5 8 e 13. Persino il numero di petali in molti fiori come le rose canine o le margherite sono sempre numeri appartenenti alla serie e solitamente 8 o 13. In una conchiglia il rapporto tra i diametri di due spire successive è esattamente pari a phi. Pari a questo numero è anche il rapporto tra le femmine ed i maschi presenti in un alveare.
Anche in architettura sono diverse le opere che seguono questa proporzione, basti pensare alla Piramide di Giza o al Partenone di Atene. Nel campo della musica, invece, se pensiamo al pianoforte, possiamo osservare che i 13 tasti delle ottave, sono divisi in 8 bianchi e 5 neri, e che, ancora, la divisione dei neri è in gruppi di 2 e 3. I numeri qui sono: 2,3,5,8 e 13. Se invece pensiamo al corpo umano, il rapporto tra l’altezza da terra di un uomo e l’altezza da terra del suo ombelico è la sezione aurea, così come la sezione aurea è anche il rapporto tra braccio ed intero arto, partendo dalla spalla, dunque comprendendo mano ed avambraccio. Partendo da questa considerazione, Leonardo da Vinci ha utilizzato la sezione aurea per costruire la sua più importante opera d’arte nel campo della scienza, ovvero l’uomo vitruviano.
Molti studiosi considerano phi come il numero più bello dell’universo.
Dello stesso avviso è Robert Langdon, protagonista del best seller “Il Codice Da Vinci” di Dan Brown. All’interno del libro, grazie alla conoscenza della successione di Fibonacci, il professor Langdon con Sophie Marceaux riescono a dissolvere il primo dilemma propostogli dal curatore del Louvre.
Il Fibonacci è colui che introdusse la numerazione araba ed il sistema decimale in Europa, facendo apparire anche il numero 0, fino ad allora entità sconosciuta. Questo avvenne all’interno dell’opera “Liber Abbaci”, nella quale sono contenute anche delle spiegazioni intorno alla sua successione e ad alcune possibili applicazioni di essa. Il matematico italiano fu il primo a verificare anche come tra un quadrato ed il successivo vi sia sempre la successione dei numeri dispari.
La grandezza di Fibonacci, però, consiste, ancora oggi, nell’essere riuscito laddove pochi altri sono stati capaci: nel mettere in relazione molto stretta i numeri, perfetti per definizione ed antonomasia, con l’irrazionale. Egli riuscì, sostanzialmente, a collegare ragionamento ed immaginazione. Per questo appare quanto mai doveroso dedicare a lui il 23.11 di ogni anno, cogliendo, quindi, la vera essenza della matematica.
P.S.: provare per credere, per curiosi ed appassionati!!!!